Compose

Description

This operation computes the composition of two transducers. If A transduces string x to y with weight a and B transduces y to z with weight b, then their composition transduces string x to z with weight a ⊗ b.

The output labels of the first transducer or the input labels of the second transducer must be sorted (or the FSTs otherwise support appropriate matchers). The weights need to form a commutative semiring (valid for TropicalWeight and LogWeight for instance).

Versions of this operation (not all shown here) accept options that allow choosing the matcher, composition filter, state table and, when delayed, the caching behavior used by composition.

Usage

template <class Arc> void Compose(const Fst<Arc> &ifst1, const Fst<Arc> &ifst2, MutableFst<Arc> *ofst);
template <class Arc> ComposeFst<Arc>:: ComposeFst(const Fst<Arc> &fst1, const Fst<Arc> &fst2);
fstcompose [--opts] a.fst b.fst out.fst --connect: Trim output (def: true)

Examples

A:

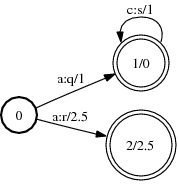
B:

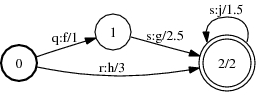
A o B:

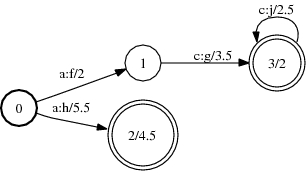
Compose(A, B, &C);
ComposeFst<Arc>(A, B);
fstcompose a.fst b.fst out.fst

Complexity

Assuming the first FST is unsorted and the second is sorted:

Compose:

• Time: O(V₁ V₂ D₁ (log D₂ + M₂))
• Space: O(V₁ V₂ D₁ M₂)
  

where V_i = # of states, D_i = maximum out-degree and M_i = maximum multiplicity for the ith FST.

ComposeFst:

• TIme: O(v₁ v₂ d₁ (log d₂ + m₂)),
• Space: O(v₁ v₂)
  

where v_i = # of states visited, d_i = maximum out-degree, and m_i = maximum multiplicity of the states visited.for the ith FST. Constant time and space to visit an input state or arc is assumed and exclusive of caching.

Caveats

Compose and fstcompose trim their output, ComposeFst does not (since it is a delayed operation).

The efficiency of composition can be strongly affected by several factors:

• the choice of which transducer is sorted
  • prefer sorting the FST that has the greater average out-degree
  • sorting both transducers allows composition to automatically select the best transducer to match against (per state pair)
  • note stored sort properties of the FSTs are first checked in constant time followed by the minimum number of linear-time sort tests necessary to discover one sorted FST; thus composition may be unaware that both FSTs are sorted when those properties are not stored.
• the amount of non-determinism
• the presence and location of epsilon transitions - avoid epsilon transitions on the output side of the first transducer or the input side of the second transducer or prefer placing them later in a path since they delay matching and can introduce non-coaccessible states and transitions

See here for more discussion on efficient usage.

See Also

Composition Filters, Matchers, State Tables