OpenFst Examples
Reading the quick tour first is recommended. That includes a simple example of FST application using either the C++ template level or the shell-level operations. The advanced usage topic contains an implementation using the template-free intermediate scripting level as well. The following data files are used in the examples below:| File | Description | Source |
|---|---|---|
| wotw.txt | (normalized) text of H.G. Well's War of the Worlds | public domain |
| wotw.lm.gz | 5-gram language model for wotw.txt in OpenFst text format |
www.opengrm.org |
| wotw.syms | FST symbol table file for wotw.lm |
www.opengrm.org |
| ascii.syms | FST symbol table file for ASCII letters | Python |
| lexicon.txt.gz | letter-to-token FST for wotw.syms |
see first example below |
| lexicon_opt.txt.gz | optimized letter-to-token FST for wotw.syms |
see first example below |
| downcase.txt | ASCII letter-to-downcased letter FST | awk 'NR>1 { print 0,0,$1,tolower($1) } ; END { print 0 }' <ascii.syms >downcase.txt |
- For the most part, we illustrate with the shell-level commands for convenience.
- The fstcompose operation is used often here. Typically, one or both of the input FSTs should be appropriately sorted before composition. In the examples below, however, we have only illustrated sorting where it is necessary, to keep the presentation shorter. The provided data files are pre-sorted for their intended use. (See Exercise 4 for more details.)
- Files with a .fst extension should be produced from their text description by a call to fstcompile. This is illustrated at the beginning, but is often implicit throughout the rest of this document.
Tokenization
The first example converts a sequence of ASCII characters into a sequence of word tokens with punctuation and whitespace stripped. To do so we will need a lexicon transducer that maps from letters to their corresponding word tokens. A simple way to generate this is using the OpenFst text format. For example, the word Mars would have the form:$ fstcompile --isymbols=ascii.syms --osymbols=wotw.syms >Mars.fst <<EOF 0 1 M Mars 1 2 a <epsilon> 2 3 r <epsilon> 3 4 s <epsilon> 4 EOFThis can be drawn with:
$ fstdraw --isymbols=ascii.syms --osymbols=wotw.syms -portrait Mars.fst | dot -Tjpg >Mars.jpgwhich produces:
 Suppose that
Suppose that Martian.fst and man.fst have similarly been created, then:
$ fstunion man.fst Mars.fst | fstunion - Martian.fst | fstclosure >lexicon.fstproduces a finite-state lexicon that transduces zero or more spelled-out word sequences into their word tokens:
$ fstrmepsilon lexicon.fst | fstdeterminize | fstminimize >lexicon_opt.fstresulting in the equvialent, deterministic and minimal:
$ fstunion man.fst Mars.fst | fstunion - Martian.fst | fstconcat - punct.fst | fstclosure >lexicon.fst
where:
$ fstcompile --isymbols=ascii.syms --osymbols=wotw.syms >punct.fst <<EOF 0 1 <space> <epsilon> 0 1 . <epsilon> 0 1 , <epsilon> 0 1 ? <epsilon> 0 1 ! <epsilon> 1 EOFis a transducer that deletes common punctuation symbols. The full punctuation transducer is here. Now, the tokenizaton of the example string Mars man encoded as an FST:
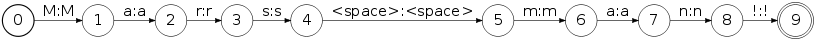 can be done with:
can be done with:
$ fstcompose Marsman.fst lexicon_opt.fst | fstproject --project_output | fstrmepsilon >tokens.fstgiving:
 Note that our construction of
Note that our construction of lexicon.fst requires that all tokens be separated by exactly one whitespace character, including at the end of the string (hence the '!' in the previous example).
To generate a full lexicon of all 7102 distinct words in the War of Worlds, it is convenient to dispense with the union
of individual word FSTs above and instead generate a single text FST from the word symbols in wotw.syms.
Here is a python script that does that and was used, along with the above steps,
to generate the full optimized lexicon (which you should compile to lexicon_opt.fst).
Exercise 1
The above tokenization does not handle numeric character input. (a) Create a transducer that maps numbers in the range 0 - 999999 represented as digit strings to their English read form, e.g.:1 -> one 11 -> eleven 111 -> one hundred eleven 1111 -> one thousand one hundred eleven 11111 -> eleven thousand one hundred eleven(b) Incorporate this transduction into the letter-to-token transduction above and apply to the input Mars is 4225 miles across. represented as letters.
Downcasing Text
The next example converts case-sensitive input to all lowercase output. To do the conversion, we create a flower transducer of the form:$ fstcompile --isymbols=ascii.syms --osymbols=ascii.syms >downcase.fst <<EOF 0 0 ! ! 0 0 A a 0 0 B b 0 0 a a 0 0 b b 0 EOFwhich produces:
 A downcasing flower transducer for the full character set is here. This transducer can be applied to the Mars men automaton from the previous example with:
A downcasing flower transducer for the full character set is here. This transducer can be applied to the Mars men automaton from the previous example with:
$ fstproject Marsman.fst | fstcompose - full_downcase.fst | fstproject --project_output >marsman.fstgiving:
 Why use transducers for this when UNIX commands like
Why use transducers for this when UNIX commands like tr and C library routines like tolower are some of the many easy ways to downcase text? Transducers have several advantages over these approaches. First, more complex transformations are almost
as easy to write (see Example 2). Second, trying to invert this transduction is less trivial and can be quite useful (see the next section).
Finally, this transducer operates on any finite-state input not just a string. For example,
$ fstinvert lexicon_opt.fst | fstcompose - full_downcase.fst | fstinvert >lexicon_opt_downcase.fstdowncases the letters in the lexicon from the previous example. A transducer that downcases at the token level (but see Exercise 3a) can be created with:
$ fstinvert lexicon_opt.fst | fstcompose - full_downcase.fst | fstcompose - lexicon_opt.fst | fstrmepsilon | fstdeterminize | fstminimize >downcase_token.fst
Exercise 2
Create a transducer that: (a) upcases letters that are string-initial or after a punctuation symbol/space (capitalization transducer). (b) converts lowercase underscore-separated identifiers such asnum_final_states to the form NumFinalStates (CamelCase transducer).
Exercise 3
(a) The letter-level downcasing transducer downcases any ASCII input. For which inputs does the token-level downcasing transducer work? What changes would be necessary to cover all inputs fromwotw.syms?
(b) If a token The were applied to downcase_token.fst, what would the output look like? What would it look like if the optimizations (epsilon-removal, determinization and minimization) were omitted from the construction of downcase_token.fst.
Exercise 4
Create a 1,000,000 ASCII character string represented as an FST. Compose it on the left withdowncase.fst and time the computation.
Compose it on the right and time the computation. The labels in downcase.fst were pre-sorted on one side; use fstinfo to
determine which side. Use fstarcsort to sort downcase.fst on the opposite side and repeat the experiments above.
Given that composition matching uses binary search on the sorted side (with the higher out-degree, if both sides are sorted), explain the differences in computation time that you observe.
Case Restoration in Text
This example creates a transducer that attempts to restore the case of downcased input. This is the first non-trivial example and, in general, there is no error-free way to do this. The approach taken here will be to use case statistics gathered from the The War of the Worlds source text to help solve this. In particular, we will use an n-gram language model created on this text that is represented as a finite-state automaton inOpenFst format, which you should compile to the file wotw.lm.fst. Here is a typical path in this 5-gram automaton:
$ fstrandgen --select=log_prob wotw.lm.fst | fstprint --isymbols=wotw.syms --osymbols=wotw.syms 0 1 The The 1 2 desolating desolating 2 3 cry cry 3 4 <epsilon> <epsilon> 4 5 worked worked 5 6 <epsilon> <epsilon> 6 7 upon upon 7 8 my my 8 9 mind mind 9 10 <epsilon> <epsilon> 10 11 once once 11 12 <epsilon> <epsilon> 12 13 <epsilon> <epsilon> 13 14 I I 14 15 <epsilon> <epsilon> 15 16 <epsilon> <epsilon> 16 17 slept slept 17 18 <epsilon> <epsilon> 18 19 little little 19This model is constructed to have a transition for every 1-gram to 5-gram seen in 'War of the Worlds' with its weight related to the (negative log) probability of that n-gram occurring in the text corpus. The epsilon transitions correspond to backoff transitions in the smoothing of the model that was performed to allow accepting input sequences not seen in training. Given this language model and using the lexicon and downcasing transducers from the previous examples, a solution is:
# Before trying this, read the whole section.
$ fstcompose lexicon_opt.fst wotw.lm.fst | fstarcsort --sort_type=ilabel >wotw.fst
$ fstinvert full_downcase.fst | fstcompose - wotw.fst >case_restore.fst
The first FST, wotw.fst, maps from letters to tokens following the probability distribution of the language model.
The second FST, case_restore.fst is similar but uses only downcased letters. Case prediction can then be performed with:
$ fstcompose marsman.fst case_restore.fst | fstshortestpath | fstproject --project_output | fstrmepsilon | fsttopsort >prediction.fstwhich gives:
 In other words, the most likely case of the input is determinized with respect to the n-gram model.
There is a serious problem, however, with the above solution. For all but tiny corpora,
the first composition is extremely expensive with the classical composition algorithm since the
output labels in
In other words, the most likely case of the input is determinized with respect to the n-gram model.
There is a serious problem, however, with the above solution. For all but tiny corpora,
the first composition is extremely expensive with the classical composition algorithm since the
output labels in lexicon_opt.fst have been pushed back when it was determinized and this greatly delays matching
with the labels in wotw.lm.fst. There are three possible solutions:
First, we can use the input to restrict the composition chain as:
$ fstcompose full_downcase.fst marsman.fst | fstinvert | fstcompose - lexicon_opt.fst | fstcompose - wotw.lm.fst | fstshortestpath | fstproject -project_output | fstrmepsilon | fsttopsort >prediction.fstThis works fine but has the disadvantage that we don't have a single transducer to apply and we are depending on the input being a string or otherwise small. A second solution, which gives a single optimized transducer, is to replace transducer determinization and minimization of lexicon.fst with automata determinization and minimization (via encoding the input and output label pairs into a single new label) followed by the transducer determinization and minimization of the result of the composition with
wotw.fst:
$ fstencode --encode_labels lexicon.fst enc.dat | fstdeterminize | fstminimize | fstencode --decode - enc.dat >lexicon_compact.fst $ fstcompose lexicon_compact.fst wotw.lm.fst | fstdeterminize | fstminimize | fstarcsort --sort_type=ilabel >wotw.fst $ fstinvert full_downcase.fst | fstcompose - wotw.fst >case_restore.fstThis solution is a natural and simple one but has the disadvantage that the transducer determinization and minimization steps are quite expensive. A final solution is to use an FST representation that allows lookahead matching, which composition can exploit to avoid the matching delays:
# Converts to a lookahead lexicon $ fstconvert --fst_type=olabel_lookahead --save_relabel_opairs=relabel.pairs lexicon_opt.fst >lexicon_lookahead.fst $ fstrelabel --relabel_ipairs=relabel.pairs wotw.lm.fst | fstarcsort --sort_type=ilabel >wotw_relabel.lm # Relabels the language model input (required by lookahead implementation) $ fstcompose lexicon_lookahead.fst wotw_relabel.lm >wotw.fst $ fstinvert full_downcase.fst | fstcompose - wotw.fst >case_restore.fstThe relabeling of the input labels of the language model is a by-product of how the lookahead matching works. Note in order to use the lookahead FST formats you must use
--enable-lookahead-fsts in the library configuration and you must set your
LD_LIBRARY_PATH (or equivalent) appropriately.
Exercise 5
(a) Find the weight of the second shortest distinct token sequence in the prediction example above. (b) Find the weight of the second shortest distinct token sequence in the prediction example above without using the--nshortest flag (hint: use fstdifference).
(c) Find all paths within weight 10 of the shortest path in prediction example.
Exercise 6
(a) The case restoration above can only work for words that are found in the text corpus. Describe an alternative that gives a plausible result on any letter sequence. (b) Punctuation can give clues to the case of nearby words (e.g. i was in cambridge, ma. before. it was nice.). Describe a method to exploit this information in case restoration.Exercise 7
Create a transducer that converts the digits 0-9 into their possible telephone keypad alphabetic equivalents (e.g., 2: a,b,c; 3: d,e,f) and allows for spaces as well. Use this transducer to convert the sentence no one would have believed in the last years of the nineteenth century that this world was being watched keenly and closely into digits and spaces. Use the lexicon alone to disambiguate this digit and space sequence (cf. T9 phone input). Now use both the lexicon and the language model to disambiguate it.Edit Distance
Since the predictions made in the previous example might not always be correct, we may want to measure the error when we have the correct reference answers as well. One common error measure is computed by aligning the hypothesis and reference, defining:edit distance = # of substitutions + # of deletions + # of insertionsand then defining
error rate = edit distance / # of reference symbolsIf this is computed on letters, it is called the letter error rate; on words, it is called the word error rate. Suppose the reference and (unweighted) hypothesis are represented as finite-state automata
ref.fst and hyp.fst respectively. Then:
$ fstcompose ref.fst edit.fst | fstcompose - hyp.fst |
# Returns shortest distance from final states to the initial (first) state
$ fstshortestdistance --reverse | head -1
computes the edit distance between the reference and hypothesis according to the edit transducer edit.fst. The edit transducer for
two letters a and b is the flower automaton:
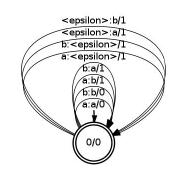 This counts any substitution (a:b, b:a), insertion (<epsilon>:a, <epsilon>:b), or deletion as (a:<epsilon>:a, b:<epsilon>) as 1 edit and matches (a:a, b:b) as zero edits. For word error rate, we use the Levenshtein edit distance, i.e. where the cost of substitutions, insertions, and deletions are all the same. However, each pairing of a symbol (or epsilon) with another symbol
can be given a separate cost in a more general edit distance. This can obviously be implemented by choosing different weights
for the corresponding edit transducer transitions. Even more general edit distances can be defined (see Exercise 8).
Note that if the hypothesis is not a string but a more general automaton representing a set of
hypotheses (e.g. the result from Exercise 5c) then this procedure returns the oracle edit distance, i.e., the edit distance of the best-matching ('oracle-provided') hypothesis
compared to the reference. The corresponding oracle error rate is a measure of the quality of the hypothesis set (often called a 'lattice').
There is one serious problem with this approach and that is when the symbol set is large. For the 95 letter
This counts any substitution (a:b, b:a), insertion (<epsilon>:a, <epsilon>:b), or deletion as (a:<epsilon>:a, b:<epsilon>) as 1 edit and matches (a:a, b:b) as zero edits. For word error rate, we use the Levenshtein edit distance, i.e. where the cost of substitutions, insertions, and deletions are all the same. However, each pairing of a symbol (or epsilon) with another symbol
can be given a separate cost in a more general edit distance. This can obviously be implemented by choosing different weights
for the corresponding edit transducer transitions. Even more general edit distances can be defined (see Exercise 8).
Note that if the hypothesis is not a string but a more general automaton representing a set of
hypotheses (e.g. the result from Exercise 5c) then this procedure returns the oracle edit distance, i.e., the edit distance of the best-matching ('oracle-provided') hypothesis
compared to the reference. The corresponding oracle error rate is a measure of the quality of the hypothesis set (often called a 'lattice').
There is one serious problem with this approach and that is when the symbol set is large. For the 95 letter ascii.syms, the
Levenstein edit transducer will have 9215 transitions. For the 7101 word wotw.syms, there would need to be
50,438,403 transitions. While this is still manageable, larger vocabularies of 100,000 and more words are unwieldy.
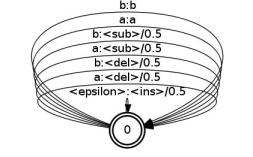
For the Levenstein distance, there is a simple solution: factor the edit transducer into two components. Using the example above, the left
factor, edit1.fst, is:
 and the right factor,
and the right factor, edit2.fst, is:
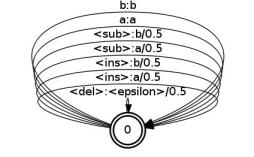 These transducers include new symbols <sub>, <del>, and <ins> that are used for the substitution, deletion and
insertion of other symbols respectively. In fact, the composition of these two transducers is equivalent to the
original edit transducer
These transducers include new symbols <sub>, <del>, and <ins> that are used for the substitution, deletion and
insertion of other symbols respectively. In fact, the composition of these two transducers is equivalent to the
original edit transducer edit.fst. However, each of these transducers has 4 |V| transitions where |V| is the number of
distinct symbols, whereas the original edit transducer has (|V|+1)2-1 transitions.
Given these factors, compute:
$ fstcompose ref.fst edit1.fst | fstarcsort >ref_edit.fst $ fstcompose edit2.fst hyp.fst | fstarcsort >hyp_edit.fst $ fstcompose ref_edit.fst hyp_edit.fst | fstshortestdistance --reverse | head -1With large inputs, the shortest distance algorithm may need to use inadmissable pruning. This is because the edit transducer allows arbitrary insertions and deletions, so the search space is quadratic in the length of the input. Alternatively the edit transducer could be changed (see Exercise 8b). With more general edit transducers, this factoring may not be possible. In that case, representing the edit transducer in some specialized compact FST representation would be possible but pairwise compositions might be very expensive. A three-way composition algorithm or specialized composition matchers and filters are approaches that could implement this more efficiently. As an example, we can see to what extent the case restoration transducer errs on a given input by computing the edit distance between the output it yields and the reference answer. We will use the Levenshtein distance. First, generate
edit1.fst and edit2.fst. These should be structured like the example above, but should provide transitions for each symbol of ascii.symb not just 'a' and 'b'. You will need to create levenshtein.symb which contains the definitions of ascii.symb plus new definitions for "<ins>", "<del>" and "<sub>". Then, prepare the transducers edit1.txt and edit2.txt as above from ascii.symb, and compile them (edit1.fst would have ascii.symb as input symbols and levenshtein.symb as output symbols, and vice versa for edit2.fst).
Create a transducer ref.fst representing a correctly capitalized English sentence using words from the corpus and with adequate whitespace. You might want to use words which appear both capitalized and uncapitalized in the source text to have a chance to observe a non-zero edit distance. A suitable (nonsensical) example is the following: "The nice chief astronomer says that both the terraces of the south tower and the western mills in the East use the English Channel as a supply pool "
You can now downcase ref.fst (with the full_downcase.fst transducer presented above), apply case_restore.fst to it and get the hypothesis output for this input (as was explained in the section about case restoration). Compose that with the reversed tokenizer to get the hypothesis represented as a sequence of characters not tokens. This is hyp.fst, which should be a FST representing a string along the lines of "The Nice chief Astronomer says that both the terraces of the south Tower and the western Mills in the east use the English channel as a Supply Pool ".
Now, you can compute the edit distance as in the example above. For the given ref.fst and hyp.fst, the edit distance should be 8. You can also show the alignment (which, in the present case, will only include substitutions):
$ fstcompose ref.fst edit1.fst | fstarcsort >ref_edit.fst $ fstcompose edit2.fst hyp.fst | fstarcsort >hyp_edit.fst $ fstcompose ref_edit.fst hyp_edit.fst | fstshortestpath | fstrmepsilon | fsttopsort | fstprint --isymbols=levenshtein.syms --osymbols=levenshtein.symsHere is the output (with some added color to make it easier to read):
0 1 T T 1 2 h h 2 3 e e 3 4 <space> <space> 4 5 n N 1 5 6 i i 6 7 c c 7 8 e e 8 9 <space> <space> 9 10 c c 10 11 h h 11 12 i i 12 13 e e 13 14 f f 14 15 <space> <space> 15 16 a A 1 16 17 s s 17 18 t t 18 19 r r 19 20 o o 20 21 n n 21 22 o o 22 23 m m 23 24 e e 24 25 r r 25 26 <space> <space> 26 27 s s 27 28 a a 28 29 y y 29 30 s s 30 31 <space> <space> 31 32 t t 32 33 h h 33 34 a a 34 35 t t 35 36 <space> <space> 36 37 b b 37 38 o o 38 39 t t 39 40 h h 40 41 <space> <space> 41 42 t t 42 43 h h 43 44 e e 44 45 <space> <space> 45 46 t t 46 47 e e 47 48 r r 48 49 r r 49 50 a a 50 51 c c 51 52 e e 52 53 s s 53 54 <space> <space> 54 55 o o 55 56 f f 56 57 <space> <space> 57 58 t t 58 59 h h 59 60 e e 60 61 <space> <space> 61 62 s s 62 63 o o 63 64 u u 64 65 t t 65 66 h h 66 67 <space> <space> 67 68 t T 1 68 69 o o 69 70 w w 70 71 e e 71 72 r r 72 73 <space> <space> 73 74 a a 74 75 n n 75 76 d d 76 77 <space> <space> 77 78 t t 78 79 h h 79 80 e e 80 81 <space> <space> 81 82 w w 82 83 e e 83 84 s s 84 85 t t 85 86 e e 86 87 r r 87 88 n n 88 89 <space> <space> 89 90 m M 1 90 91 i i 91 92 l l 92 93 l l 93 94 s s 94 95 <space> <space> 95 96 i i 96 97 n n 97 98 <space> <space> 98 99 t t 99 100 h h 100 101 e e 101 102 <space> <space> 102 103 E e 1 103 104 a a 104 105 s s 105 106 t t 106 107 <space> <space> 107 108 u u 108 109 s s 109 110 e e 110 111 <space> <space> 111 112 t t 112 113 h h 113 114 e e 114 115 <space> <space> 115 116 E E 116 117 n n 117 118 g g 118 119 l l 119 120 i i 120 121 s s 121 122 h h 122 123 <space> <space> 123 124 C c 1 124 125 h h 125 126 a a 126 127 n n 127 128 n n 128 129 e e 129 130 l l 130 131 <space> <space> 131 132 a a 132 133 s s 133 134 <space> <space> 134 135 a a 135 136 <space> <space> 136 137 s S 1 137 138 u u 138 139 p p 139 140 p p 140 141 l l 141 142 y y 142 143 <space> <space> 143 144 p P 1 144 145 o o 145 146 o o 146 147 l l 147 148 <space> <space> 148
Exercise 8
Create an edit transducer that: (a) allows only a fixed number N of contiguous insertions or deletions. (b) computes the Levenshtein distance between American and English spellings of words except that common spelling variantsExercise 9
Provide a way to: (a) compute the error rate rather than the edit distance using transducers. (b) compute the oracle error path as well as the oracle rate for a lattice.| I | Attachment | History | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|---|
| |
Mars.jpg | r1 | manage | 10.8 K | 2010-12-08 - 06:15 | MichaelRiley | |
| |
Marsman.png | r3 r2 r1 | manage | 13.0 K | 2010-12-09 - 01:52 | MichaelRiley | |
| |
ascii.syms | r2 r1 | manage | 0.5 K | 2010-12-08 - 06:06 | MichaelRiley | |
| |
downcase.jpg | r2 r1 | manage | 3.8 K | 2010-12-08 - 23:39 | MichaelRiley | |
| |
edit.jpg | r1 | manage | 6.4 K | 2010-12-10 - 03:37 | MichaelRiley | |
| |
edit1.jpg | r3 r2 r1 | manage | 8.2 K | 2011-03-31 - 01:29 | UnknownUser | |
| |
edit2.jpg | r3 r2 r1 | manage | 8.1 K | 2011-03-31 - 01:29 | UnknownUser | |
| |
full_downcase.txt | r2 r1 | manage | 0.8 K | 2010-12-08 - 22:48 | MichaelRiley | |
| |
full_punct.txt | r1 | manage | 0.7 K | 2010-12-09 - 01:42 | MichaelRiley | |
| |
lexicon.jpg | r3 r2 r1 | manage | 15.6 K | 2012-06-11 - 22:58 | UnknownUser | |
| |
lexicon.png | r5 r4 r3 r2 r1 | manage | 18.4 K | 2010-12-08 - 07:06 | MichaelRiley | |
| |
lexicon.txt.gz | r1 | manage | 300.9 K | 2010-12-09 - 06:39 | MichaelRiley | |
| |
lexicon_opt.txt.gz | r2 r1 | manage | 226.2 K | 2010-12-09 - 02:27 | MichaelRiley | |
| |
lexiconmin.png | r1 | manage | 20.1 K | 2010-12-08 - 07:06 | MichaelRiley | |
| |
makelex.py.txt | r1 | manage | 0.4 K | 2010-12-08 - 08:48 | MichaelRiley | |
| |
marsman.png | r2 r1 | manage | 12.9 K | 2010-12-09 - 02:11 | MichaelRiley | |
| |
prediction2.png | r2 r1 | manage | 16.1 K | 2010-12-10 - 02:39 | MichaelRiley | |
| |
tokens.jpg | r1 | manage | 4.5 K | 2010-12-09 - 02:09 | MichaelRiley | |
| |
tokens.png | r2 r1 | manage | 14.4 K | 2010-12-08 - 07:47 | MichaelRiley | |
| |
wotw.lm.gz | r1 | manage | 3331.7 K | 2010-12-08 - 05:28 | MichaelRiley | |
| |
wotw.syms | r1 | manage | 88.8 K | 2010-12-08 - 05:13 | MichaelRiley | |
| |
wotw.txt | r1 | manage | 331.0 K | 2010-12-08 - 05:11 | MichaelRiley |
Topic revision: r22 - 2017-02-15 - KyleGorman
Ideas, requests, problems regarding TWiki? Send feedback

