ShortestPath
Description
This operation produces an FST containing the n -shortest paths in the input FST. The n -shortest paths are the n -lowest weight paths w.r.t. the natural semiring order. The single path that can be read from the ith of at most n transitions leaving the initial state of the resulting FST is the ith shortest path. The weights need to be right distributive and have the path property. They also need to be left distributive as well for n -shortest with n > 1 (valid forTropicalWeight).
Usage
template<class Arc> void ShortestPath(const Fst<Arc> &ifst, MutableFst<Arc> *ofst, size_t n = 1); |
fstshortestpath [--opts] a.fst out.fst
--nshortest: type = int64, default = 1
Return N-shortest paths
--unique: default = false
Return only distinct strings (NB: must be acceptor; epsilons treated as regular symbols)
|
Examples
A:
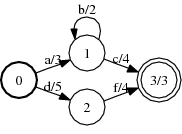 (TropicalWeight)
(TropicalWeight)
Shortest path in A:
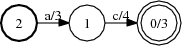
2-shortest paths in A:

Complexity
ShortestPath: - 1-shortest path:
- Time: O(V log V + E)
- Space: O(V)
- n-shortest paths:
- Time: O(V log V + n V + n E)
- Space: O(n V)
Caveats
See here for a discussion on efficient usage.See Also
ShortestDistance, State QueuesReferences
- Mehryar Mohri. Semiring Framework and Algorithms for Shortest-Distance Problems
 , Journal of Automata, Languages and Combinatorics, 7(3):321-350, 2002.
, Journal of Automata, Languages and Combinatorics, 7(3):321-350, 2002.
- Mehryar Mohri and Michael Riley. An Efficient Algorithm for the n-best-strings problem
 , In Proceedings of the International Conference on Spoken Language Processing 2002 (ICSLP '02).
, In Proceedings of the International Conference on Spoken Language Processing 2002 (ICSLP '02).
| I | Attachment | History | Action | Size |
Date | Who | Comment |
|---|---|---|---|---|---|---|---|
| |
shortestpath2.jpg | r1 | manage | 6.1 K | 2007-07-09 - 20:50 | CyrilAllauzen | 1-shortest path example |
| |
shortestpath1.jpg | r1 | manage | 9.4 K | 2007-07-09 - 20:50 | CyrilAllauzen | shortest path input example |
| |
shortestpath3.jpg | r1 | manage | 18.5 K | 2007-07-09 - 20:51 | CyrilAllauzen | 2-shortest path example |
This topic: FST > WebHome > FstQuickTour > ShortestPathDoc
Topic revision: r11 - 2018-04-27 - MichaelRiley
Ideas, requests, problems regarding TWiki? Send feedback

