Pynini documentation
,ggggggggggg,
dP"""88""""""Y8,
Yb, 88 `8b
`" 88 ,8P gg gg
88aaaad8P" "" ""
88""""" gg gg ,ggg,,ggg, gg ,ggg,,ggg, gg
88 I8 8I ,8" "8P" "8, 88 ,8" "8P" "8, 88
88 I8, ,8I I8 8I 8I 88 I8 8I 8I 88
88 ,d8b, ,d8I ,dP 8I Yb,_,88,_,dP 8I Yb,_,88,_
88 P""Y88P"8888P' 8I `Y88P""Y88P' 8I `Y88P""Y8
,d8I'
,dP'8I
,8" 8I
I8 8I
`8, ,8I
`Y8P"
Introduction
Pynini (Gorman 2016, Gorman & Sproat 2021) is a library for compiling a grammar of strings, regular expressions, and context-dependent rewrite rules into weighted finite-state transducers.Design
Pynini supports much of the functionality of Thrax, but whereas Thrax is essentially a compiler for a domain-specific language, Pynini is implemented as a Python extension module. This provides several advantages:- Pynini users can exploit Python's rich tooling ecosystem, including logging and unit testing frameworks.
- Pynini users can incorporate Thrax primitives like string compilation into executables.
Outline
This document covers the following areas:- formal preliminaries underlying finite-state transducers,
- getting started with Pynini,
- examples of Pynini in action,
- API reference, and
- advanced topics.
Formal preliminaries
Finite-state transducers (FSTs) are models of computation widely used for speech and language processing:- Speech recognition: language models, the pronunciation dictionaries, and the lattices produced by the acoustic model are all represented as FSTs; combined, these define the hypothesis space for the recognizer.
- Speech synthesis: FSTs are used for text normalization, the phase of linguistic analysis that converts written text like "meet me at St. Catherine on Bergen St. @ 9:30" to a pronounceable utterance like "meet me at the Saint Catherine on Bergen Street at nine thirty".
- Natural language processing: FSTs are used to represent sequence models such as those used for part of speech tagging, noun chunking, and named entity recognition.
- Information retrieval: finite automata are used to detect dates, times, etc., in web text.
State machines
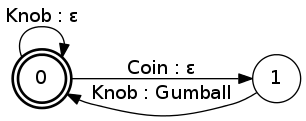
Finite automata are simply state machines with a finite number of states. And, a state machine is any devices whose behavior can be modeled using transitions between a number of states. While our finite automata are implemented in software, there are also hardware state machines, like the traditional gumball machine (image credit: Wikimedia Commons): A working gumball machine can be in one of two states: either its coin slot does, or does not, contain a coin. Initially the gumball machine has an empty coin slot; and turning the knob has no effect on the state of the machine. But once a coin is inserted into the coin slot, turning the knob dispenses a gumball and empties the coin slot. If the knob is turned while the coin slot is vacant, no change of state occurs. However, if the knob is turned while the coin slot is occupied, a gumball is dispensed and the coin slot is cleared. We can represent this schematic description of a gumball machine as a directed graph in which the states are represented by circles and the transitions between states—henceforth, arcs—are represented by arrows between states. Each arc has a pair of labels representing the input consumed, and output emitted, respectively, when that arc is traversed. By convention, the Greek letter ε (epsilon) is used to represent null input and/or output along an arc.
A working gumball machine can be in one of two states: either its coin slot does, or does not, contain a coin. Initially the gumball machine has an empty coin slot; and turning the knob has no effect on the state of the machine. But once a coin is inserted into the coin slot, turning the knob dispenses a gumball and empties the coin slot. If the knob is turned while the coin slot is vacant, no change of state occurs. However, if the knob is turned while the coin slot is occupied, a gumball is dispensed and the coin slot is cleared. We can represent this schematic description of a gumball machine as a directed graph in which the states are represented by circles and the transitions between states—henceforth, arcs—are represented by arrows between states. Each arc has a pair of labels representing the input consumed, and output emitted, respectively, when that arc is traversed. By convention, the Greek letter ε (epsilon) is used to represent null input and/or output along an arc.
 The bold double-circle state labeled
The bold double-circle state labeled 0 simply indicates that that state is "final", whereas the single-circle state 1 is non-final. Here, this encodes the notion that no user would walk away from a gumball machine while there's still a coin in the slot.
Finite-state acceptors
In what follows, we draw heavily from chapter 1 of Roark & Sproat 2008, and interested readers are advised to consult that resource for further details.Definition
Finite-state acceptors (or FSAs) are the simplest type of FST. Each FSA represents a set of strings (henceforth, a language), similar to a regular expression, as follows. An FSA consists of a five-tuple (Q, S, F, Σ δ) where:- Q is a finite set of states,
- S is the set of start states,
- F is the set of final states,
- Σ is the alphabet, and
- δ : Q × (Σ ∪ ε) → Q is the transition relation.
- The source state for p0 is in S,
- δ(qi li) = qi + 1 for any pi = (qi, li, qi + 1) ∈ P, and
- the destination state for pn is in F.
Example
The following FSA represents the Perl-style regular expressionab*cd+e:
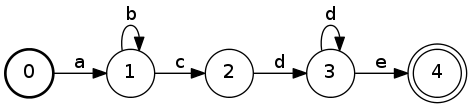 Here, the bold circle labeled
Here, the bold circle labeled 0 indicates the start state, and the double
circle labeled 4 indicates the final state.
Finite-state transducers
Definition
Finite-state transducers (FSTs) are generalization of FSAs. In the normal case of a two-way transducer, δ is instead a relation from Q × (Σi ∪ ε) × (Σo ∪ ε) → Q where Σiand Σo are the input and output alphabets, respectively. Paths through a FST are defined similarly to the definition given for FSAs above, except that each path corresponds to a set of two strings, an input string over Σi* and an output string over Σo*. Whereas FSAs describe sets of strings, FSTs describe relations between sets of strings. When the relation described by an FST is such that each input string corresponds to at most one output string, we say that the FST is functional.Example
The following FST represents the relation(a:a)(b:b)*(c:g)(d:f)+(e:e):
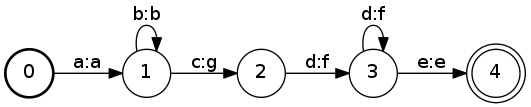
Weighted finite-state transducers
Definition
Weighted finite-state transducers (WFSTs) are generalizations of FSTs which use an alternative definition of both F and δ incorporating the notion of weights. FST weights and their operations can be understood by first defining the notion of semiring, which require us to first define the notion monoid. A monoid is a pair (M, •) where M is a set and • is a binary operation on M such that:- • is closed over M: for all a, b in M, a • b ∈ M,
- there is an identity element e ∈ M such that a • e = e • = a for all a ∈ M, and
- • is associative; for all a, b, c ∈ M, (a • b) • c = a • (b • c).
- (𝕂, ⊕) is a commutative monoid,
- (𝕂, ⊗) is a monoid,
- for all a, b, c ∈ 𝕂, a ⊗ (b ⊕ c) = (a ⊗ b) ⊕ (a ⊗ c), and
- for all a ∈ 𝕂, a ⊗ 0 = 0 ⊗ a = 0 where 0 is the identity element for the monoid (𝕂, ⊕).
standard arc type) is the default semiring in Pynini.
At last, we can give the modified definitions for F and delta; for WFSTs. Whereas for unweighted FSTs, F is a set of final states, for WFSTs F is a set of pairs over Q × 𝕂, where the second element is the final weight for that state. And, the transition relation δ for a WFST is from Q × (Σi ∪ ε) × (Σo ∪ ε) × 𝕂 to Q. The definition of paths is parallel to those for unweighted FSTs except that each element in the path is also associated with a weight in 𝕂.
Example
WFSTs are a natural representation for conditional probability distributions from strings to strings. For example, consider a text normalization rule which verbalizes2:00 as two with P = .2 and as two o'clock with P = .8. The following probability (i.e., real-valued) semiring WFST encodes this distribution:

Conventions used in Pynini
- Pynini represents all acceptors and transducers, weighted or unweighted, as WFSTs. Thus, for example, a weighted finite-state acceptor (WFSA) is represented as a WFST in which input and output labels match in all cases, and an unweighted finite-state transducer is represented by a WFST in which all weights are 1 or 0.
- Pynini only permits one state to be designated the start state.
- Pynini assigns a final weight to all states; a nonfinal state is just one which has a final weight of 0.
Getting started with Pynini
Starting Pynini
Install Pyniniimport pynini
Building FSTs
In Pynini, all FST objects are an instance of a class calledpynini.Fst, representing a mutable WFST. The user must specify the arc type at construction time; by default, the standard arc type (and the associated tropical semiring) is are used.
Pynini provides several functions for compiling strings into FSTs; we proceed to review a few of these methods.
Constructing acceptors
Theacceptor function compiles a (Unicode or byte) string into a deterministic acceptor. The user may specify a final weight using the weight keyword argument; by default, the final weight is 1. The user may also specify the desired arc type using the arc_type keyword argument. The user may also specify how the characters in the string are to be translated into labels of the acceptor. By default (token_type="byte"), each arc in the acceptor corresponds to byte in the input string. Finally, the user may specify whether or not the symbol table used should be attached to the FST using the attach_symbols keyword argument, which defaults to True.
# UTF-8 bytestring, byte arcs.
print(pynini.accep("Pont l'Evêque"))
# Output below...
0 1 80 80
1 2 111 111
2 3 110 110
3 4 116 116
4 5 32 32
5 6 108 108
6 7 39 39
7 8 69 69
8 9 118 118
9 10 195 195
10 11 170 170
11 12 113 113
12 13 117 117
13 14 101 101
14
If the user specifies token_type="utf8" then each arc in the FST corresponds to a Unicode codepoint.
# UTF-8 bytestring, Unicode codepoint arcs.
print(pynini.accep("Pont l'Evêque", token_type="utf8"))
# Output below...
0 1 80 80
1 2 111 111
2 3 110 110
3 4 116 116
4 5 32 32
5 6 108 108
6 7 39 39
7 8 69 69
8 9 118 118
9 10 195 195
10 11 170 170
11 12 113 113
12 13 117 117
13 14 101 101
14
Sequences of characters enclosed by [ and ] receive special interpretations in byte or utf8 mode. Pynini first attempts to parse any such sequence as an integer using the C standard library function strtoll.
assert pynini.accept("b[0x61][97]") == pynini.accep("baa") # OK.
If this fails, then Pynini treats the sequence as a sequence of one or more whitespace-delimited "generated" symbols, each of which is given a unique identifier in the resulting FST's symbol table.
x = pynini.accep("[It's not much of a cheese shop really]")
y = pynini.accep("[It's][not][much][of][a][cheese][shop][really]")
assert x == y # OK.
A bracket character to be interpreted literally must be escaped.
bracket = pynini.accep("\[") # OK.
unused = pynini.accep("[") # Not OK: Raises FstStringCompilationError.
Finally, if the user specifies a SymbolTable as the token_type, then the input string is parsed according and the FST labeled according to that table. String parsing failures are logged and raise a FstStringCompilationError exception from within the Python interpreter.
Nearly all FST operations permit a string to be passed in place of an Fst argument; in that case, pynini.acceptor is used (with default arguments) to compile the string into an FST.
Constructing transducers
Thecross function creates a transducer from two FSTs, compiling string arguments into FSTs if necessary. The result is a cross-product of the two input FSTs, interpreted as acceptors. Specifically, the transducer is constructed by mapping output arcs in the first FST to epsilon, mapping the input arcs in the second FST to epsilon, then concatenating the two. In the case that both FSTs are strings, the resulting transducer will simply contain the input and output string converted into labels, and the shorter of the two will be padded with epsilons.
As with acceptor, the user may specify a final weight using the weight keyword argument; the final weight is 1. The user also specify the desired arc type using the arc_type keyword argument. The user may also specify how the characters in the input and/or output strings are to be translated into labels of the transducer, if strings are passed in place of FST arguments. By default (input_token_type="byte" and output_token_type="byte"), each arc corresponds to a byte in the input and/or output string. Finally, the user may specify whether or not symbol tables should be attached to the FST.
Whereas cross is used to construct the cross-product of two strings or automata, the union of many string pair cross-products is compiled using the string_map and string_file functions. The former takes iterables of strings as an argument; the latter reads string pairs from one-to-three TSV filearc_type keyword argument.
Worked examples
The following examples, taken from Gorman 2016 and Gorman & Sproat 2016, show features of Pynini in action.Finnish vowel harmony
Koskenniemi (1983) provides a number of manually-compiled FSTs modeling Finnish morphophonological patterns. One of these concerns the well-known pattern of Finnish vowel harmony. Many Finnish suffixes have two allomorphs differing only in the backness specification of their vowel. For example, the adessive suffix is usually realized as -llä [lːæː] except when the preceding stem contains one of u, o, and a and there is no intervening y, ö, or ä; in this case, it is -lla [lːɑː]. For example, käde 'hand' has an adessive kädellä, whereas vero 'tax' forms the adessive verolla because the nearest stem vowel is o ( Ringen & Heinämäki 1999). The following gives a Pynini functionmake_adessive which generates the appropriate form of the noun stem. It first concatenates the stem with an abstract representation of the suffix, and then composes the result with a context-dependent rewrite rule adessive_harmony.
back_vowel = pynini.union("u", "o", "a")
neutral_vowel = pynini.union("i", "e")
front_vowel = pynini.union("y", "ö", "ä")
vowel = pynini.union(back_vowel, neutral_vowel, front_vowel)
archiphoneme = pynini.union("A", "I", "E", "O", "U")
consonant = pynini.union("b", "c", "d", "f", "g", "h", "j", "k", "l", "m", "n",
"p", "q", "r", "s", "t", "v", "w", "x", "z")
sigma_star = pynini.union(vowel, consonant, archiphoneme).closure()
adessive = "llA"
intervener = pynini.union(consonant, neutral_vowel).closure()
adessive_harmony = (pynini.cdrewrite(pynini.cross("A", "a"),
back_vowel + intervener, "", sigma_star) @
pynini.cdrewrite(pynini.cross("A", "ä"), "", "", sigma_star)
).optimize()
def make_adessive(stem):
ur = stem + adessive
sr = ur @ adessive_harmony
return sr.string()
T9 disambiguation
T9 (short for "Text on 9 keys"; Grover et al. 1998) is a patented predictive text entry system. In T9, each character in the "plaintext" alphabet is assigned to one of the 9 digit keys (0 is usually reserved to represent space) of the traditional 3x4 touch-tone phone grid. For instance, the message GO HOME is entered as 4604663. Since the resulting "ciphertext" may be highly ambiguous—this sequence could also be read as GO HOOD or as many nonsensical expressions—a hybrid language model/lexicon is used for decoding. The following snippet implements T9 encoding and decoding in Pynini:
LM = pynini.Fst.read("charlm.fst")
T9_ENCODER = pynini.string_file("t9.tsv").closure()
T9_DECODER = pynini.invert(T9_ENCODER)
def encode_string(plaintext):
return (plaintext @ T9_ENCODER).string()
def k_best(ciphertext, k):
lattice = ciphertext @ T9_DECODER
lattice.project("output")
lattice @= LM
return pynini.shortestpath(lattice, nshortest=k, unique=True)
The first line reads a language model (LM), represented as a WFSA. The second line reads the encoder table from a TSV file: in this file, each line contains an alphabetic character and the corresponding digit key. By computing the concatenative closure of this map, one obtains an FST T9_ENCODER which can encode arbitrarily-long plaintext strings. The encode_string function applies this FST to arbitrary plaintext strings: application here refers to composition of a string with a transducer followed by output projection. The
k_best function first applies a ciphertext string—a bytestring of digits—to the inverse of the encoder FST (T9_DECODER). This creates an intermediate lattice of all possible plaintexts consistent with the T9 ciphertext. This is then scored with—that is, composed with—the character LM. Finally, this function returns the k highest probability plaintexts in the lattice. For the following example, the highest probability plaintext is in fact the correct one:
pt = "THE SINGLE MOST POPULAR CHEESE IN THE WORLD"
ct = encode_string(pt)
print("CIPHERTEXT:", ct)
print("DECIPHERED PLAINTEXT:", k_best(ct, 1).string())
---+ Output below...
CIPHERTEXT: 8430746453066780767852702433730460843096753
DECIPHERED PLAINTEXT: THE SINGLE MOST POPULAR CHEESE IN THE WORLD
API reference 
The APIs are documented in-module. To learn about a function or method, use Python's built-in help function (or in Jupyter, use the ? prefix operator); e.g., import pynini; help(pynini).
References
Gorman, Kyle. 2016. Pynini: A Python library for weighted finite-state grammar compilationTopic revision: r33 - 2022-07-10 - KyleGorman
Ideas, requests, problems regarding TWiki? Send feedback
